問題・問題用紙は東京都教育委員会のHPからプリントアウトしてください。https://www.kyoiku.metro.tokyo.lg.jp/admission/high_school/ability_test/problem_and_answer/release20200221_01.html
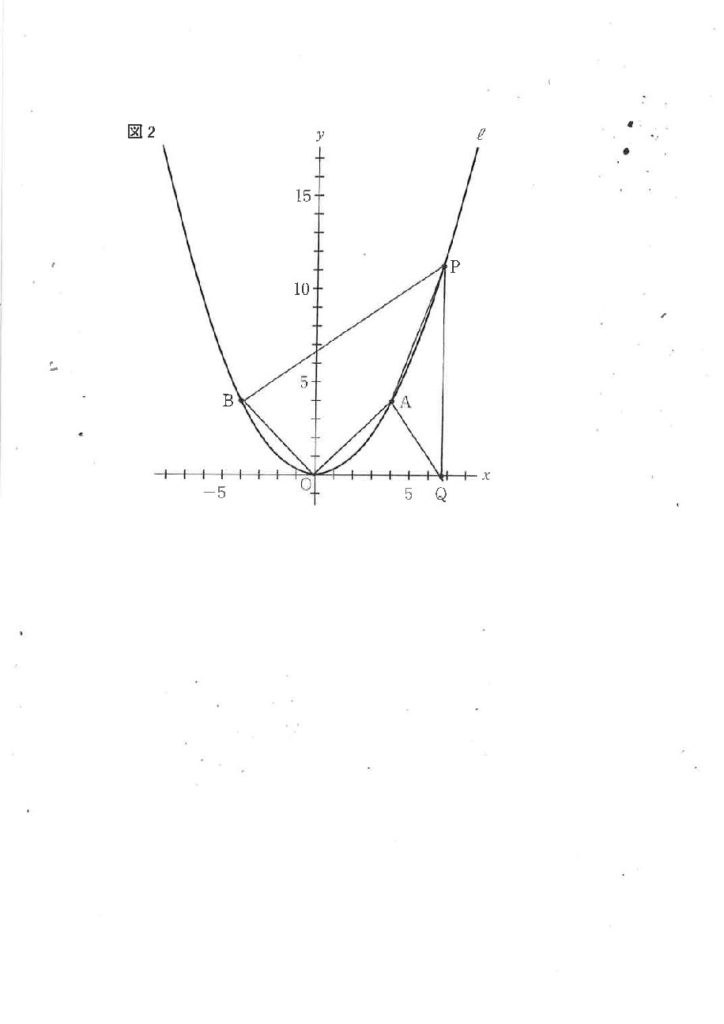
A( 4 , 4 )
点Bはy軸を対称の軸として線対称な点なので
B ( -4 , 4 )となる。
ここで、点Qの座標を( t, 0 )とおく。
点Pと点Qのx座標は等しいので、点Pの座標をtを用いて表すと
P( t, 1/4 t^2 )と表せられる。
次に四角形OAPBの面積について考える。
四角形OAPB = △ABP+ △OABなので
△OABは底辺をABとすると面積は 8×4×1/2 = 16
△ABPも底辺をABとすると面積はtを用いて表すと
8×( 1/4 t^2 – 4 ) ×1/2 となる。
よって△ABP = t^2 – 16
ここで四角形OAPBは 16 + t^2 – 16 = t^2 となる。
△AOQは底辺をOQとすると面積はtを用いて表すと
t× 4 × 1/2 = 2t となる。
ここでの問題の題意は四角形OAPBの面積が△AOQの面積の 4倍になるときなので
t^2 = 8t となる。
よって t^2 – 8t = 0
t ( t – 8 ) = 0
t = 0 , 8
ただし、題意より点Pのx座標は 4 より大きいので
t = 8 となる
よって 点Pのx座標は 8 となる。







